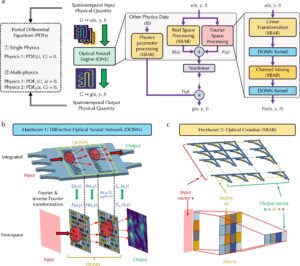
Partial differential equations (PDEs) are a class of mathematical problems that represent the interplay of multiple variables, and therefore have predictive power when it comes to complex physical systems. Solving these equations is a perpetual challenge, however, and current computational techniques for doing so are time-consuming and expensive.
Now, research from the University of Utah’s John and Marcia Price College of Engineering is showing a way to speed up this process: encoding those equations in light and feeding them into their newly designed “optical neural engine,” or ONE.
The researchers’ ONE combines diffractive optical neural networks and optical matrix multipliers. Rather than representing PDEs digitally, the researchers represented them optically, with variables represented by the various properties of a light wave, such as its intensity and phase. As a wave passes through the ONE’s series of optical components, those properties gradually shift and change, until they ultimately represent the solution to the given PDE.
The study was led by Weilu Gao, assistant professor in the Department of Electrical & Computer Engineering, and Ruiyang Chen, a Ph.D. candidate in Gao’s research group. They collaborated with Yingheng Tang and Zhi Yao, Research Scientists in the Computing Sciences Area at Lawrence Berkeley National Laboratory (LBNL). Yingheng Tang is a former member of the Gao group. Other authors include other Gao lab members Minhan Lou and Jichao Fan, the University of Maryland’s Cunxi Yu, as well as Andrew Nonaka from LBNL.
They published a study demonstrating this optical neural engine in the journal Nature Communications.
“Partial differential equations are a powerful computational tool to simulate physics problems instead of performing expensive and time-consuming real-world experiments,” says Chen. “However, the current numerical simulation method is slow and requires a lot of computing resources, and even electronic machine learning techniques are not fast enough.”
The machine learning techniques and digital neural networks currently used to solve PDEs involve passing the equation through a network of computational nodes, each of which weights its output as it passes it on to the next node. As the signal makes its way through the network, the correct solution becomes weighted most heavily and ends up as the output.
The researchers’ ONE takes this concept and applies it to photonic devices.
“The ONE takes the spatiotemporal data of an input physical quantity, which is a function of positions and time, to predict the spatiotemporal data of an output physical quantity as a function of positions and time,” explains Gao.
Electronic machine learning techniques can produce a similar output, but at slower speeds and higher energy costs.
“This optical approach accelerates the machine learning process and requires less energy as compared to an electronic approach,” says Tang.
The researchers demonstrated their ONE’s capabilities on a number of PDEs, including the Darcy flow equation, the magnetostatic Poisson’s equation in demagnetization, and the Navier-Stokes equation in incompressible fluid.
“The Darcy flow equation, for example, describes a fluid flow through a porous medium,” says Gao. “Given data about the permeability and pressure fields inside a given medium, the ONE architecture essentially learns the mapping between those qualities, and can predict flow properties without having to experiment.”
“This research offers a versatile and powerful platform for large-scale scientific and engineering computation, such as geology and chip design,” says Gao.
The research was supported by the National Science Foundation through Grants No. 2235276, No. 2316627, and No. 2428520, the University of Utah start-up fund, the US Department of Energy, Office of Science, Office of Advanced Scientific Computing Research, the Microelectronics Science Research Center Projects for Energy Efficiency and Extreme Environments, under contract no. DE-AC02-05-CH11231, and Laboratory Directed Research and Development funding from Berkeley Lab, provided by the Director, Office of Science, of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231. This research used resources of the National Energy Research Scientific Computing Center (NERSC), a DOE Office of Science User Facility supported by the Office of Science of the U.S. Department of Energy under Contract No. DE-AC02-05CH11231, and under NERSC GenAI award under No. DDR-ERCAP0030541.